Welcome to little lamb

Find the first (most significant) bit set in C

Posted

Here's a simple problem in appearance : how to find the first bit set in a number ? Or, the most significant bit set ?

It's a question I got confronted with, and of course the answer doesn't seem that complicated. In fact, it's pretty simple to imagine how one can achieve this : just start from the left and loop until the first bit.

Sure enough, that'll do the trick. But is it really ideal ? It feels that one could optimize this a bit, and if you're gonna find yourself needed to look for that first bit quite often, you might want a better (read: faster) solution.

The solutions

Method 0: A very naive approach

As we've seen earlier, the most basic/naive solution is just to shift until we found that special bit Or, to right shift until we got to zero, meaning we just got rid of the MSB, and since we took care of counting how many steps/shifts were necessary, we know its looked-after position.

1
2
3
4
5
6
7
8
9
cint msb(u64 v)
{
    if (!v) return 0;

    int n;
    for(n = 0; v >>= 1; ++n)
        ;
    return n + 1;
}

I'm also adding the special case of zero, to make sure we get the expected result all the time. This will be present in about all methods.

Method 1: Shift only if necessary

Now the previous method is there as a reference really, since it will be slow. Or, it might be slow, or fast, depending on which is the mighty msb. Indeed, it can find it after only one shift, or it could need more than sixty of them.

A better solution might be to check : if anything is set in the upper 32 bits, then shift them down, and add 32 to our count. If anything is set in the upper 16 bits - of our now 32-bit number - then shift them down, and add 16 to our count. And so on until we're down to the last bit.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
cint msb(u64 v)
{
    if (!v) return 0;

    int k = 0;
    if (v > 0xFFFFFFFFUL) { v >>= 32; k  = 32; }
    if (v > 0x0000FFFFUL) { v >>= 16; k |= 16; }
    if (v > 0x000000FFUL) { v >>= 8;  k |= 8;  }
    if (v > 0x0000000FUL) { v >>= 4;  k |= 4;  }
    if (v > 0x00000003UL) { v >>= 2;  k |= 2;  }
    if (v > 0x00000001UL) { k |= 1; }

    return k + 1;
}

Method 2: Same as before, but with a precomputed table of log2

Another alternative - originally by VoidStar - is based on the same principle at first, but instead of going all the way down we stop at one byte (8 bits), and then use a table lookup to get our result.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
cconst u8 kTableLog2[256] = {
0,0,1,1,2,2,2,2,3,3,3,3,3,3,3,3,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,
5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,
6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,
6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,
7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,
7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,
7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,
7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7
};

int msb(u64 v)
{
    if (!v) return 0;

    int  k = 0;
    if (v > 0xFFFFFFFFUL) { v >>= 32; k  = 32; }
    if (v > 0x00FFFFFFUL) { v >>= 24; k |= 24; }
    if (v > 0x0000FFFFUL) { v >>= 16; k |= 16; }
    if (v > 0x000000FFUL) { v >>=  8; k |=  8; }
    k |= kTableLog2[v]; /* precompute the Log2 of the low byte */

    return k + 1;
}

Method 3: A fixed number of steps

Another approach, from an anonymous poster, is to use a fixed number of steps, always. This will be slower at times, but maybe faster at others (especially compared to our naive method 0).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
cint msb(u64 v)
{
    if (!v) return 0;

    u64 msb  = 32;
    u64 step = msb;
    while (step > 1)
    {
        step /= 2;
        if (v >> msb)
            msb += step;
        else
            msb -= step;
    }
    if (v >> msb)
        ++msb;

    return msb;
}

Method 4: Data-driven binary search

Kaz Kylheku proposed a solution implementing a "data-driven binary search"

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
cint msb(u64 v)
{
  const long long mask[] = {
    0x00000000FFFFFFFF,
    0x000000000000FFFF,
    0x00000000000000FF,
    0x000000000000000F,
    0x0000000000000003,
    0x0000000000000001
  };
  int hi = 64;
  int lo = 0;
  int i = 0;

  if (v == 0)
    return 0;

  for (i = 0; i < sizeof mask / sizeof mask[0]; i++) {
    int mi = lo + (hi - lo) / 2;

    if ((v >> mi) != 0)
      lo = mi;
    else if ((v & (mask[i] << lo)) != 0)
      hi = mi;
  }

  return lo + 1;
}

Method 5: Unrolled decision tree

Another solution proposed by Kaz Kylheku was a "completely unrolled decision tree by hand", which makes for a very large amount of code that feels impossible to maintain, but has no loops nor tables.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
cint msb(u64 n)
{
    if (n & 0xFFFFFFFF00000000) {
        if (n & 0xFFFF000000000000) {
            if (n & 0xFF00000000000000) {
                if (n & 0xF000000000000000) {
                    if (n & 0xC000000000000000)
                        return (n & 0x8000000000000000) ? 64 : 63;
                    else
                        return (n & 0x2000000000000000) ? 62 : 61;
                } else {
                    if (n & 0x0C00000000000000)
                        return (n & 0x0800000000000000) ? 60 : 59;
                    else
                        return (n & 0x0200000000000000) ? 58 : 57;
                }
            } else {
                if (n & 0x00F0000000000000) {
                    if (n & 0x00C0000000000000)
                        return (n & 0x0080000000000000) ? 56 : 55;
                    else
                        return (n & 0x0020000000000000) ? 54 : 53;
                } else {
                    if (n & 0x000C000000000000)
                        return (n & 0x0008000000000000) ? 52 : 51;
                    else
                        return (n & 0x0002000000000000) ? 50 : 49;
                }
            }
        } else {
            if (n & 0x0000FF0000000000) {
                if (n & 0x0000F00000000000) {
                    if (n & 0x0000C00000000000)
                        return (n & 0x0000800000000000) ? 48 : 47;
                    else
                        return (n & 0x0000200000000000) ? 46 : 45;
                } else {
                    if (n & 0x00000C0000000000)
                        return (n & 0x0000080000000000) ? 44 : 43;
                    else
                        return (n & 0x0000020000000000) ? 42 : 41;
                }
            } else {
                if (n & 0x000000F000000000) {
                    if (n & 0x000000C000000000)
                        return (n & 0x0000008000000000) ? 40 : 39;
                    else
                        return (n & 0x0000002000000000) ? 38 : 37;
                } else {
                    if (n & 0x0000000C00000000)
                        return (n & 0x0000000800000000) ? 36 : 35;
                    else
                        return (n & 0x0000000200000000) ? 34 : 33;
                }
            }
        }
    } else {
        if (n & 0x00000000FFFF0000) {
            if (n & 0x00000000FF000000) {
                if (n & 0x00000000F0000000) {
                    if (n & 0x00000000C0000000)
                        return (n & 0x0000000080000000) ? 32 : 31;
                    else
                        return (n & 0x0000000020000000) ? 30 : 29;
                } else {
                    if (n & 0x000000000C000000)
                        return (n & 0x0000000008000000) ? 28 : 27;
                    else
                        return (n & 0x0000000002000000) ? 26 : 25;
                }
            } else {
                if (n & 0x0000000000F00000) {
                    if (n & 0x0000000000C00000)
                        return (n & 0x0000000000800000) ? 24 : 23;
                    else
                        return (n & 0x0000000000200000) ? 22 : 21;
                } else {
                    if (n & 0x00000000000C0000)
                        return (n & 0x0000000000080000) ? 20 : 19;
                    else
                        return (n & 0x0000000000020000) ? 18 : 17;
                }
            }
        } else {
            if (n & 0x000000000000FF00) {
                if (n & 0x000000000000F000) {
                    if (n & 0x000000000000C000)
                        return (n & 0x0000000000008000) ? 16 : 15;
                    else
                        return (n & 0x0000000000002000) ? 14 : 13;
                } else {
                    if (n & 0x0000000000000C00)
                        return (n & 0x0000000000000800) ? 12 : 11;
                    else
                        return (n & 0x0000000000000200) ? 10 : 9;
                }
            } else {
                if (n & 0x00000000000000F0) {
                    if (n & 0x00000000000000C0)
                        return (n & 0x0000000000000080) ? 8 : 7;
                    else
                        return (n & 0x0000000000000020) ? 6 : 5;
                } else {
                    if (n & 0x000000000000000C)
                        return (n & 0x0000000000000008) ? 4 : 3;
                    else
                        return (n & 0x0000000000000002) ? 2 : (n ? 1 : 0);
                }
            }
        }
    }
}

Method 6: Magic. Also known as "de Bruijn sequence"

I'm not even gonna try to describe what a de Bruijn sequence is, mostly because i would be incapable of it, but if you're curious I'll point you to Wikipedia, often a good place to start.

Anyways, this solution involves a few bit shift, a multiplication with a magic number and a magical table that pops out the answer we're looking for. It's wonderfully awesome. :-)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
cconst u8 index64[64] = {
    0, 47,  1, 56, 48, 27,  2, 60,
    57, 49, 41, 37, 28, 16,  3, 61,
    54, 58, 35, 52, 50, 42, 21, 44,
    38, 32, 29, 23, 17, 11,  4, 62,
    46, 55, 26, 59, 40, 36, 15, 53,
    34, 51, 20, 43, 31, 22, 10, 45,
    25, 39, 14, 33, 19, 30,  9, 24,
    13, 18,  8, 12,  7,  6,  5, 63
};

int msb(u64 v)
{
    if (!v) return 0;

    const u64 debruijn64 = 0x03F79D71B4CB0A89UL;

    v |= v >> 1;
    v |= v >> 2;
    v |= v >> 4;
    v |= v >> 8;
    v |= v >> 16;
    v |= v >> 32;

    return index64[(v * debruijn64) >> 58] + 1;
}

Solution by Kim Walisch & Mark Dickinson.

Method 7: Another de Bruijn sequence

From Niklas B. comes a little variation on the previous method, with different magic number & associated tables, this time with 128 entries.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
cconst u8 bitPatternToLog2[128] = {
     0, 48, -1, -1, 31, -1, 15, 51,
    -1, 63,  5, -1, -1, -1, 19, -1,
    23, 28, -1, -1, -1, 40, 36, 46,
    -1, 13, -1, -1, -1, 34, -1, 58,
    -1, 60,  2, 43, 55, -1, -1, -1,
    50, 62,  4, -1, 18, 27, -1, 39,
    45, -1, -1, 33, 57, -1,  1, 54,
    -1, 49, -1, 17, -1, -1, 32, -1,
    53, -1, 16, -1, -1, 52, -1, -1,
    -1, 64,  6,  7,  8, -1,  9, -1,
    -1, -1, 20, 10, -1, -1, 24, -1,
    29, -1, -1, 21, -1, 11, -1, -1,
    41, -1, 25, 37, -1, 47, -1, 30,
    14, -1, -1, -1, -1, 22, -1, -1,
    35, 12, -1, -1, -1, 59, 42, -1,
    -1, 61,  3, 26, 38, 44, -1, 56
};

int msb(u64 v)
{
    v |= v >> 1;
    v |= v >> 2;
    v |= v >> 4;
    v |= v >> 8;
    v |= v >> 16;
    v |= v >> 32;
    return bitPatternToLog2[(u64)(v * 0x6C04F118E9966F6BUL) >> 57];
}

Also notice one less addition, as the table already contains the "proper" value.

Method 8: de Bruijn for 32bit

I'll be honest, this one wasn't there originally. But after a first bunch of tests, it turned out the de Bruijn solutions seemed pretty slow on 32bit.

So, I thought what could be interesting is another another method that would first check if the there's anything in the upper 32 bits, if so shift them down, then do its magic on a 32bit value. For the sake of 32bit systems.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
cconst u8 table[32] =
{
     0,  9,  1, 10, 13, 21,  2, 29,
    11, 14, 16, 18, 22, 25,  3, 30,
     8, 12, 20, 28, 15, 17, 24,  7,
    19, 27, 23,  6, 26,  5,  4, 31
};

int msb(u64 v)
{
    if (!v) return 0;

    u32 v32;
    u8 n;
    if (v > 0xFFFFFFFF) {
        v32 = v >> 32;
        n = 33;
    } else {
        v32 = v;
        n = 1;
    }

    v32 |= v32 >> 1;
    v32 |= v32 >> 2;
    v32 |= v32 >> 4;
    v32 |= v32 >> 8;
    v32 |= v32 >> 16;

    return n + table[(v32 * 0x07C4ACDDU) >> 27];
}

With thanks to Jim Mischel for providing the magic number & associated table for the de Bruijn sequence.

Method 9: Assembler

I've heard that assembler was faster than C, so let's have a try with a bit of inline assembler. This might not be portable or really usable as-is - also it's not supported on 32bit systems - but it'll let us see how other methods compare at least.

1
2
3
4
5
6
7
8
9
cint msb(u64 v)
{
    long n = -1;

    __asm__("bsrq %1,%0"
        : "+r" (n)
        : "rm" (v));
    return n + 1;
}

Method 10: GCC builtin

Oh yeah, even though there are no functions in C to do what we're looking for, GCC comes with a nice builtin that does almost what we want. It will not tell use what the first bit set is, but it will tell us how many leading zeroes there are.

Which, to be fair, is pretty much the same thing. (Assuming you know how many bits you're dealing with.)

1
2
3
4
5
cint msb(u64 v)
{
    if (!v) return 0;
    return 64 - __builtin_clzll(v);
}

Might be worthy to note that Clang also supports it.

Testing

Now that we have a little bunch of different implementations, let's run some tests. Of course that might not be as easy as it sounds, and I'm by no means an expert on the subject - far from it.

Tests

So, here's what I came up with :

1
2
3
4
5
6
7
8
9
10
11
12
13
cint total = 0;

int main(void)
{
    for(int i = 4200000; i > 0; --i) {
        for(int l = 0; l < 64; ++l) {
            u64 n = 1ULL << l;
            total += msb(n - 1) + msb(n) + msb(n + 1);
        }
    }

    return 0;
}

It seemed pretty much okay to me, looping a bunch of times over a few values, making sure to hit all possible bits.

Alternative Tests

Having said all that, during my research I found a post by David Howells when optimization for a similar problem was introduced in the Linux kernel. (It was about making use, when possible, of the previously mentioned asm call.)

Along with the changes was the code he used for testing, and so I figured I might as well borrow it for our tests. Here's how it went :

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
cint total = 0;

/* By David Howells */

#define PAGE_SHIFT 12
static int
get_msb(u64 v)
{
    int r;
    --v;
    v >>= PAGE_SHIFT;
    r = msb(v);
    return r;
}

int main(void)
{
    long rep, loop;
    u64 v;

    for (rep = 1000000; rep > 0; --rep) {
        for (loop = 0; loop <= 16384; loop += 4) {
            v = 1UL << loop;
            total += get_msb(v);
        }
    }

    return 0;
}

And with that, we're good to go.

Results

Yeah, the good parts. And to make them look better, I even did some nice graphs to look at ! ;-)

As hinted earlier, I ran those tests on a 64bit CPU, as well as on some old 32bit one. I also wanted to see the differences between results with & without optimizations, so I ran them first with -O0, and then with -O3.

Obviously the later is really where things matter, but it might be worth something anyhow.

On to the good stuff...

Tests, i686, -O0

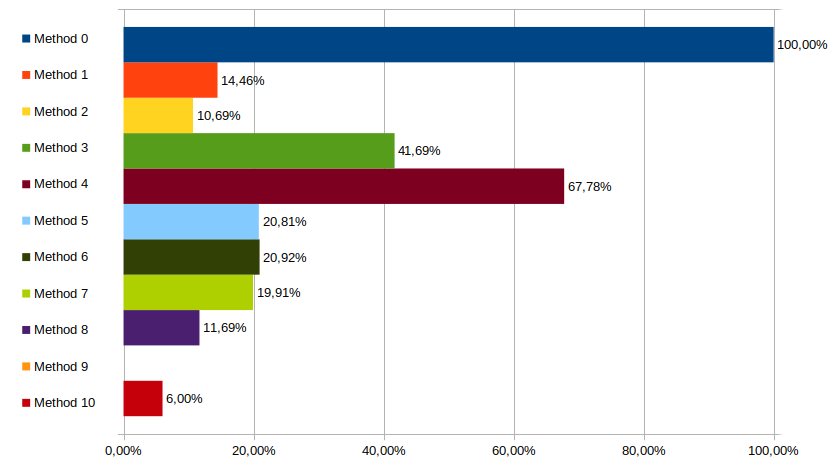
As expected our methods 1 & 2 perform much better than the naive method 0. They do pretty damn well in fact.

The unrolled tree is pretty good as well, whilst the de Bruijn methods don't do bad, but not as good.as methods 1 & 2. Of course, method 8 - our de Bruijn on a 32bit value - does much better. In fact, it does better then method 1, and gets pretty close to method 2.

Alternative Tests, i686, -O0

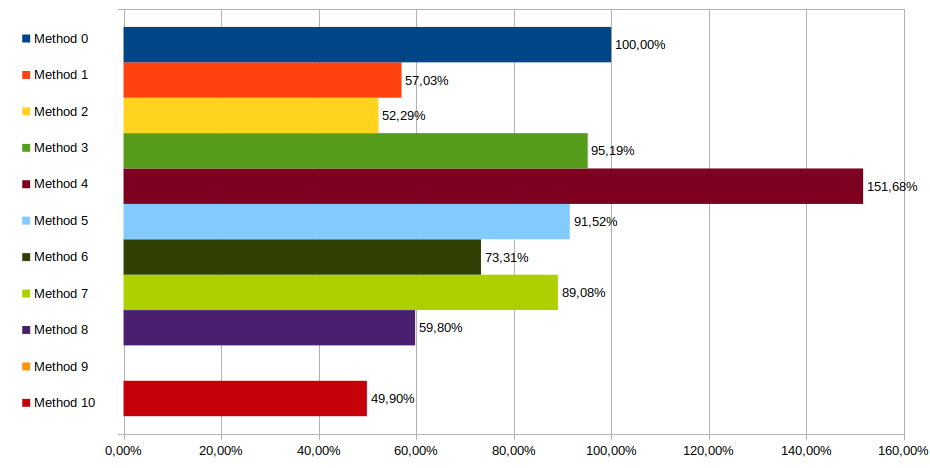
We do get some different results from those alternative tests. First off, method 4 completely tanks and manages to be worse then our naive implementation !

Methods 1 & 2 are still pretty solid, cutting time in half almost, and this time beat the de Bruijn methods, including the 32bit one (method 8).

Interestingly the unrolled tree took a hit there.

Tests, i686, -O3

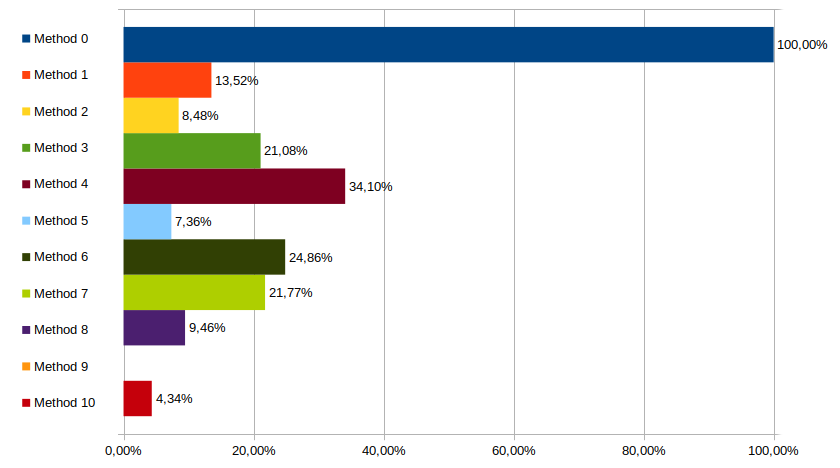
Okay now thing get serious, optimizations are in, this is real stuff. And it makes quite a difference. Especially on the unrolled tree, which now takes the lead, being the best performer of all C solutions (only beaten by the GCC builtin).

Methods 1 & 2 remain very strong candidates, and we see that the de Bruijn performs very nicely is 32bit mode (method 8), much better than when dealing with full 64bit numbers.

Alternative Tests, i686, -O3

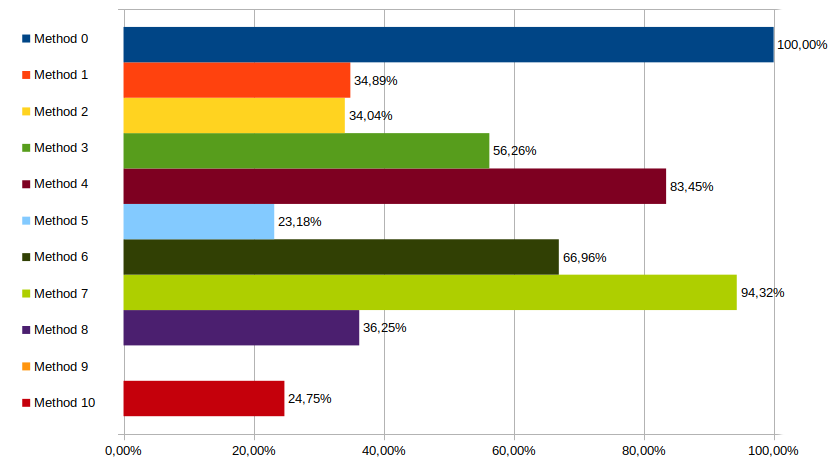
This time things get somewhat consistent with alternative tests : the unrolled tree remain the fastest solution, close to GCC's builtin. Methods 1 & 2 are still close behind, and de Bruijn sequence does well in 32bit, not so much otherwise - method 7 turning pretty awful.

Tests, x64, -O0

A preview of things for 64bit CPU now. Again, we start off without optimizations. Still, the unrolled tree does much better there, being the fastest solution already.

Methods 1 & 2 are not far behind, and de Bruijn sequences do much better now, with the method 8 doing barely better than method 6, and beaten by method 7.

Alternative Tests, x64, -O0

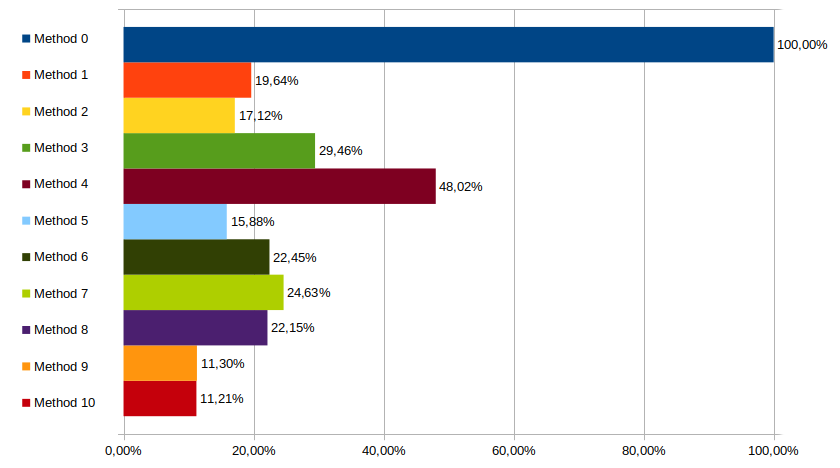
Alternative tests don't really change much this time around, except for method 7 that becomes the slowest of the de Bruijn methods, after have been the be fastest.

Other then that, same picture really.

Tests, x64, -O3

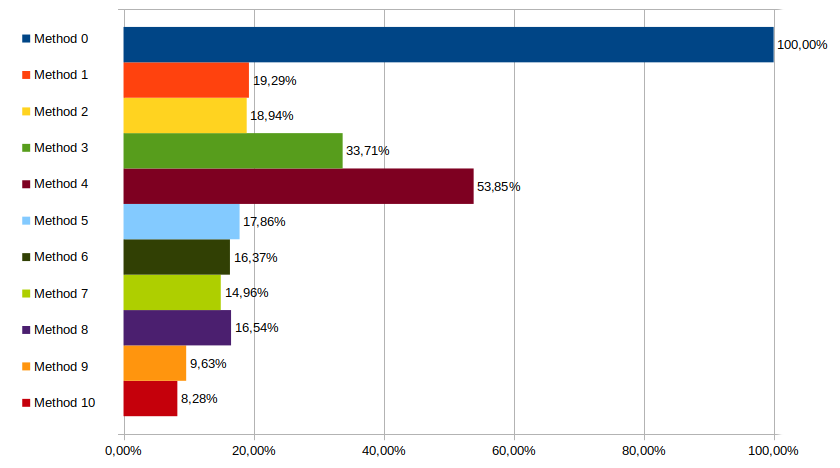
With optimizations turned on things remain mostly the same, except method 5 taking a hit. It's no longer the better performer of the bunch, de Bruijn methods all outperforming it.

It does better then methods 1 & 2 though.

Alternative Tests, x64, -O3

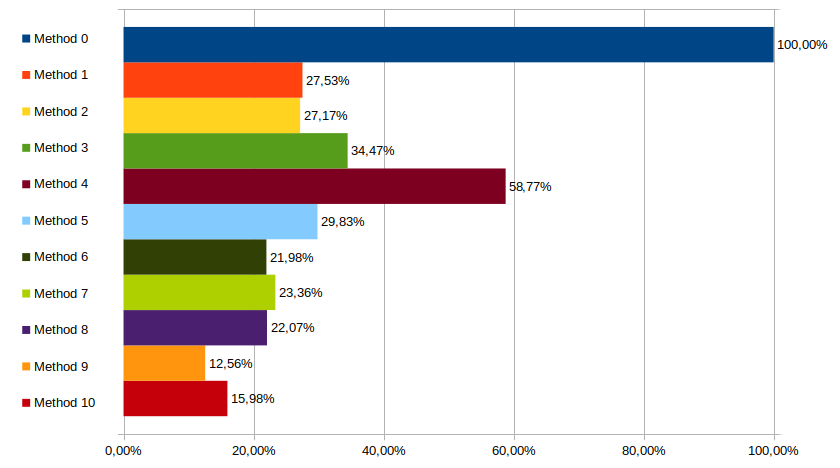
Similarly with -O0 the unrolled tree takes a little hit, as methods 1 & 2 manage to outperform it this time around.

Doesn't matter though, de Bruijn sequences are still faster. Once again method 7 doesn't like those alternative tests, being the slowest of the bunch after being the fastest in the previous/regular tests.

Conclusion

I'll let you decide whatever you want to decide, but as for me here's my takeaway :

Of course, all that is only as a fallback, for when GCC's builtin isn't available. If it is, use that, it it by far the fastest solution. (Well, there's the case of the unrolled tree during alternative tests, but let's not focus too much on that.)

Data

And just for the sake of it, or curious mind who'd like to know the figures behind those colorful bars, here it goes :

Tests, i686, -O0

1
2
3
method-0real    4m18.357s
user    4m18.209s
sys     0m0.016s

1
2
3
method-1real    0m37.353s
user    0m37.327s
sys     0m0.004s

1
2
3
method-2real    0m27.614s
user    0m27.591s
sys     0m0.008s

1
2
3
method-3real    1m47.706s
user    1m47.576s
sys     0m0.052s

1
2
3
method-4real    2m55.110s
user    2m54.997s
sys     0m0.020s

1
2
3
method-5real    0m53.766s
user    0m53.710s
sys     0m0.028s

1
2
3
method-6real    0m54.055s
user    0m53.985s
sys     0m0.044s

1
2
3
method-7real    0m51.447s
user    0m51.419s
sys     0m0.000s

1
2
3
method-8real    0m30.191s
user    0m30.173s
sys     0m0.004s

1
method-9-

1
2
3
method-10real    0m15.499s
user    0m15.482s
sys     0m0.008s

Alternative Tests, i686, -O0

1
2
3
method-0real    6m39.975s
user    6m39.764s
sys     0m0.008s

1
2
3
method-1real    3m48.096s
user    3m47.861s
sys     0m0.108s

1
2
3
method-2real    3m29.154s
user    3m28.685s
sys     0m0.148s

1
2
3
method-3real    6m20.741s
user    6m20.543s
sys     0m0.012s

1
2
3
method-4real    10m6.677s
user    10m6.106s
sys     0m0.272s

1
2
3
method-5real    6m6.043s
user    6m5.781s
sys     0m0.080s

1
2
3
method-6real    4m53.229s
user    4m53.075s
sys     0m0.008s

1
2
3
method-7real    5m56.285s
user    5m56.068s
sys     0m0.036s

1
2
3
method-8real    3m59.190s
user    3m59.008s
sys     0m0.064s

1
method-9-

1
2
3
method-10real    3m19.603s
user    3m19.507s
sys     0m0.000s

Tests, i686, -O3

1
2
3
method-0real    2m36.216s
user    2m36.132s
sys     0m0.004s

1
2
3
method-1real    0m21.116s
user    0m21.101s
sys     0m0.004s

1
2
3
method-2real    0m13.248s
user    0m13.239s
sys     0m0.000s

1
2
3
method-3real    0m32.923s
user    0m32.892s
sys     0m0.012s

1
2
3
method-4real    0m53.264s
user    0m53.201s
sys     0m0.036s

1
2
3
method-5real    0m11.502s
user    0m11.495s
sys     0m0.000s

1
2
3
method-6real    0m38.839s
user    0m38.790s
sys     0m0.020s

1
2
3
method-7real    0m34.009s
user    0m33.988s
sys     0m0.004s

1
2
3
method-8real    0m14.783s
user    0m14.774s
sys     0m0.000s

1
method-9-

1
2
3
method-10real    0m6.787s
user    0m6.779s
sys     0m0.004s

Alternative Tests, i686, -O3

1
2
3
method-0real    3m22.678s
user    3m22.533s
sys     0m0.036s

1
2
3
method-1real    1m10.705s
user    1m10.645s
sys     0m0.012s

1
2
3
method-2real    1m8.993s
user    1m8.919s
sys     0m0.040s

1
2
3
method-3real    1m54.035s
user    1m53.969s
sys     0m0.008s

1
2
3
method-4real    2m49.139s
user    2m48.946s
sys     0m0.104s

1
2
3
method-5real    0m46.988s
user    0m46.958s
sys     0m0.004s

1
2
3
method-6real    2m15.708s
user    2m15.547s
sys     0m0.076s

1
2
3
method-7real    3m11.160s
user    3m10.967s
sys     0m0.100s

1
2
3
method-8real    1m13.470s
user    1m13.428s
sys     0m0.004s

1
method-9-

1
2
3
method-10real    0m50.154s
user    0m50.102s
sys     0m0.028s

Tests, x64, -O0

1
2
3
method-0real    0m59.915s
user    0m59.886s
sys     0m0.000s

1
2
3
method-1real    0m4.731s
user    0m4.728s
sys     0m0.000s

1
2
3
method-2real    0m4.104s
user    0m4.102s
sys     0m0.000s

1
2
3
method-3real    0m10.634s
user    0m10.629s
sys     0m0.000s

1
2
3
method-4real    0m19.450s
user    0m19.440s
sys     0m0.000s

1
2
3
method-5real    0m3.235s
user    0m3.234s
sys     0m0.000s

1
2
3
method-6real    0m5.959s
user    0m5.956s
sys     0m0.000s

1
2
3
method-7real    0m5.707s
user    0m5.704s
sys     0m0.000s

1
2
3
method-8real    0m5.912s
user    0m5.904s
sys     0m0.004s

1
2
3
method-9real    0m1.834s
user    0m1.833s
sys     0m0.000s

1
2
3
method-10real    0m1.957s
user    0m1.952s
sys     0m0.004s

Alternative Tests, x64, -O0

1
2
3
method-0real    3m21.213s
user    3m21.114s
sys     0m0.003s

1
2
3
method-1real    0m39.527s
user    0m39.504s
sys     0m0.003s

1
2
3
method-2real    0m34.447s
user    0m34.429s
sys     0m0.000s

1
2
3
method-3real    0m59.282s
user    0m59.221s
sys     0m0.003s

1
2
3
method-4real    1m36.618s
user    1m36.559s
sys     0m0.000s

1
2
3
method-5real    0m31.948s
user    0m31.924s
sys     0m0.000s

1
2
3
method-6real    0m45.172s
user    0m45.140s
sys     0m0.000s

1
2
3
method-7real    0m49.552s
user    0m49.512s
sys     0m0.003s

1
2
3
method-8real    0m44.560s
user    0m44.532s
sys     0m0.000s

1
2
3
method-9real    0m22.735s
user    0m22.721s
sys     0m0.000s

1
2
3
method-10real    0m22.559s
user    0m22.548s
sys     0m0.000s

Tests, x64, -O3

1
2
3
method-0real    0m13.805s
user    0m13.798s
sys     0m0.000s

1
2
3
method-1real    0m2.663s
user    0m2.662s
sys     0m0.000s

1
2
3
method-2real    0m2.615s
user    0m2.613s
sys     0m0.000s

1
2
3
method-3real    0m4.653s
user    0m4.651s
sys     0m0.000s

1
2
3
method-4real    0m7.434s
user    0m7.430s
sys     0m0.000s

1
2
3
method-5real    0m2.465s
user    0m2.461s
sys     0m0.003s

1
2
3
method-6real    0m2.260s
user    0m2.258s
sys     0m0.000s

1
2
3
method-7real    0m2.065s
user    0m2.063s
sys     0m0.000s

1
2
3
method-8real    0m2.284s
user    0m2.282s
sys     0m0.000s

1
2
3
method-9real    0m1.330s
user    0m1.329s
sys     0m0.000s

1
2
3
method-10real    0m1.143s
user    0m1.142s
sys     0m0.000s

Alternative Tests, x64, -O3

1
2
3
method-0real    0m53.292s
user    0m53.268s
sys     0m0.000s

1
2
3
method-1real    0m14.670s
user    0m14.662s
sys     0m0.000s

1
2
3
method-2real    0m14.478s
user    0m14.469s
sys     0m0.000s

1
2
3
method-3real    0m18.371s
user    0m18.359s
sys     0m0.003s

1
2
3
method-4real    0m31.318s
user    0m31.304s
sys     0m0.000s

1
2
3
method-5real    0m15.898s
user    0m15.872s
sys     0m0.013s

1
2
3
method-6real    0m11.713s
user    0m11.702s
sys     0m0.000s

1
2
3
method-7real    0m12.449s
user    0m12.442s
sys     0m0.000s

1
2
3
method-8real    0m11.763s
user    0m11.756s
sys     0m0.000s

1
2
3
method-9real    0m6.696s
user    0m6.688s
sys     0m0.000s

1
2
3
method-10real    0m8.514s
user    0m8.510s
sys     0m0.000s

DIY: All the code

One last word, if you're curious about this and would like to ran those tests yourself/on your own hardware : it's all available on a nice little git repository. :)

The code can be browsed right here online, or you can just close the repo : git clone git://lila.oss/test-msb.git

And as a convenience, here's a tarball if you don't wanna use git.